LDA求解之变分推断EM算法

1. 变分推断EM算法求解LDA的思路

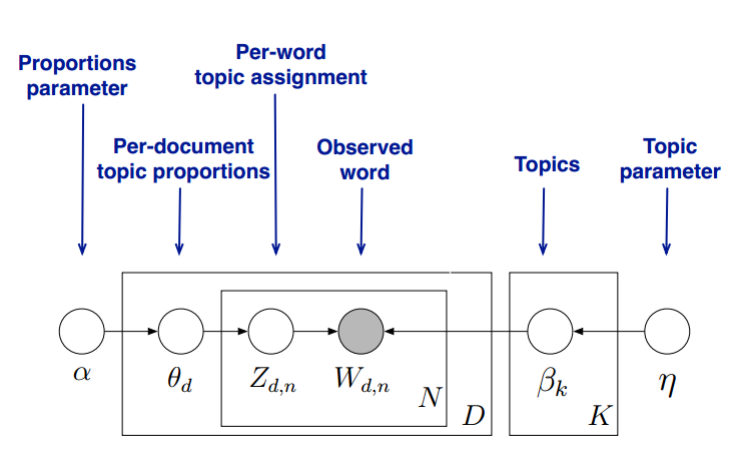
首先，回顾LDA的模型图如下：

变分推断EM算法希望通过“变分推断(Variational Inference)”和EM算法来得到LDA模型的文档主题分布和主题词分布。首先来看EM算法在这里的使用，我们的模型里面有隐藏变量$$\theta,\beta, z$$，模型的参数是$$\alpha,\eta$$。为了求出模型参数和对应的隐藏变量分布，EM算法需要在E步先求出隐藏变量$$\theta,\beta, z$$的基于条件概率分布的期望，接着在M步极大化这个期望，得到更新的后验模型参数$$\alpha,\eta$$。

问题是在EM算法的E步，由于$$\theta,\beta, z$$的耦合，我们难以求出隐藏变量$$\theta,\beta, z$$的条件概率分布，也难以求出对应的期望，需要“变分推断“来帮忙，这里所谓的变分推断，也就是在隐藏变量存在耦合的情况下，我们通过变分假设，即假设所有的隐藏变量都是通过各自的独立分布形成的，这样就去掉了隐藏变量之间的耦合关系。我们用各个独立分布形成的变分分布来模拟近似隐藏变量的条件分布，这样就可以顺利的使用EM算法了。

当进行若干轮的E步和M步的迭代更新之后，我们可以得到合适的近似隐藏变量分布$$\theta,\beta, z$$和模型后验参数$$\alpha,\eta$$，进而就得到了我们需要的LDA文档主题分布和主题词分布。

可见要完全理解LDA的变分推断EM算法，需要搞清楚它在E步变分推断的过程和推断完毕后EM算法的过程。

2. LDA的变分推断思路

要使用EM算法，我们需要求出隐藏变量的条件概率分布如下：$$p(\theta,\beta, z | w, \alpha, \eta) = \frac{p(\theta,\beta, z, w| \alpha, \eta)}{p(w|\alpha, \eta)}$$

前面讲到由于\theta,\beta, z之间的耦合，这个条件概率是没法直接求的，但是如果不求它就不能用EM算法了。怎么办呢，我们引入变分推断，具体是引入基于mean field assumption的变分推断，这个推断假设所有的隐藏变量都是通过各自的独立分布形成的，如下图所示：

我们假设隐藏变量$$\theta$$是由独立分布$$\gamma$$形成的，隐藏变量z是由独立分布$$\phi$$形成的，隐藏变量$$\beta$$是由独立分布$$\lambda$$形成的。这样我们得到了三个隐藏变量联合的变分分布q为：$$\begin{aligned} q(\beta, z, \theta|\lambda,\phi, \gamma) & = \prod_{k=1}Kq(\beta_k|\lambda_k)\prod_{d=1}Mq(\theta_d, z_d|\gamma_d,\phi_d) & = \prod_{k=1}Kq(\beta_k|\lambda_k)\prod_{d=1}M(q(\theta_d|\gamma_d)\prod_{n=1}^{N_d}q(z_{dn}| \phi_{dn})) \end{aligned}$$

我们的目标是用$$q(\beta, z, \theta|\lambda,\phi, \gamma)$$来近似的估计$$p(\theta,\beta, z | w, \alpha, \eta)$$，也就是说需要这两个分布尽可能的相似，用数学语言来描述就是希望这两个概率分布之间有尽可能小的KL距离，即：$$(\lambda*,\phi, \gamma^) = arg ;min(\lambda,\phi, \gamma);; D(q(\beta, z, \theta|\lambda,\phi, \gamma) || p(\theta,\beta, z | w, \alpha, \eta))$$

其中D(q||p)即为KL散度或KL距离，对应分布q和p的交叉熵。即：$$D(q||p) = \sum\limits_{x}q(x)log\frac{q(x)}{p(x)} = E_{q(x)}(log;q(x) - log;p(x))$$

我们的目的就是找到合适的$$\lambda*,\phi, \gamma^,$$然后用$$q(\beta, z, \theta|\lambda*,\phi, \gamma^)$$来近似隐藏变量的条件分布$$p(\theta,\beta, z | w, \alpha, \eta)$$，进而使用EM算法迭代。

这个合适的$$\lambda*,\phi, \gamma^,$$也不是那么好求的，怎么办呢？我们先看看我能文档数据的对数似然函数$$log(w|\alpha,\eta)$$如下,为了简化表示，我们用$$E_q(x)$$代替$$E_{q(\beta, z, \theta|\lambda,\phi, \gamma) }(x)$$，用来表示x对于变分分布$$q(\beta, z, \theta|\lambda,\phi, \gamma)$$的期望。

$$\begin{aligned} log(w|\alpha,\eta) & = log \int\int \sum\limits_z p(\theta,\beta, z, w| \alpha, \eta) d\theta d\beta \ & = log \int\int \sum\limits_z \frac{p(\theta,\beta, z, w| \alpha, \eta) q(\beta, z, \theta|\lambda,\phi, \gamma)}{q(\beta, z, \theta|\lambda,\phi, \gamma)}d\theta d\beta \ & = log;E_q \frac{p(\theta,\beta, z, w| \alpha, \eta) }{q(\beta, z, \theta|\lambda,\phi, \gamma)} \ & \geq E_q; log\frac{p(\theta,\beta, z, w| \alpha, \eta) }{q(\beta, z, \theta|\lambda,\phi, \gamma)} \ & = E_q; log{p(\theta,\beta, z, w| \alpha, \eta) } - E_q; log{q(\beta, z, \theta|\lambda,\phi, \gamma)} \end{aligned}$$

其中，从第(5)式到第(6)式用到了Jensen不等式：$$f(E(x)) \geq E(f(x)) ;; f(x)$$为凹函数

我们一般把第(7)式记为：$$L(\lambda,\phi, \gamma; \alpha, \eta) = E_q; log{p(\theta,\beta, z, w| \alpha, \eta) } - E_q; log{q(\beta, z, \theta|\lambda,\phi, \gamma)}$$

由于$$L(\lambda,\phi, \gamma; \alpha, \eta)$$是我们的对数似然的一个下界（第6式），所以这个L一般称为ELBO(Evidence Lower BOund)。那么这个ELBO和我们需要优化的的KL散度有什么关系呢？注意到：$$\begin{aligned} D(q(\beta, z, \theta|\lambda,\phi, \gamma) || p(\theta,\beta, z | w, \alpha, \eta)) & = E_q logq(\beta, z, \theta|\lambda,\phi, \gamma) - E_q log p(\theta,\beta, z | w, \alpha, \eta) \& =E_q logq(\beta, z, \theta|\lambda,\phi, \gamma) - E_q log \frac{p(\theta,\beta, z, w| \alpha, \eta)}{p(w|\alpha, \eta)} \& = - L(\lambda,\phi, \gamma; \alpha, \eta) + log(w|\alpha,\eta) \end{aligned}$$

在(10)式中，由于对数似然部分和我们的KL散度无关，可以看做常量，因此我们希望最小化KL散度等价于最大化ELBO。那么我们的变分推断最终等价的转化为要求ELBO的最大值。现在我们开始关注于极大化ELBO并求出极值对应的变分参数$$\lambda,\phi, \gamma$$。

3. 极大化ELBO求解变分参数

为了极大化ELBO，我们首先对ELBO函数做一个整理如下：

$$\begin{aligned} L(\lambda,\phi, \gamma; \alpha, \eta) & = E_q[logp(\beta|\eta)] + E_q[logp(z|\theta)] + E_q[logp(\theta|\alpha)] \ & + E_q[logp(w|z, \beta)] - E_q[logq(\beta|\lambda)] \ & - E_q[logq(z|\phi)] - E_q[logq(\theta|\gamma)] \end{aligned}$$

可见展开后有7项，现在我们需要对这7项分别做一个展开。为了简化篇幅，这里只对第一项的展开做详细介绍。在介绍第一项的展开前，我们需要了解指数分布族的性质。指数分布族是指下面这样的概率分布：$$p(x|\theta) = h(x) exp(\eta(\theta)*T(x) -A(\theta))$$

其中，A(x)为归一化因子，主要是保证概率分布累积求和后为1，引入指数分布族主要是它有下面这样的性质：$$\frac{d}{d \eta(\theta)} A(\theta) = E_{p(x|\theta)}[T(x)]$$

这个证明并不复杂，这里不累述。我们的常见分布比如Gamma分布，Beta分布，Dirichlet分布都是指数分布族。有了这个性质，意味着我们在ELBO里面一大推的期望表达式可以转化为求导来完成，这个技巧大大简化了计算量。

回到我们ELBO第一项的展开如下：

$$\begin{aligned} E_q[logp(\beta|\eta)] & = E_q[log(\frac{\Gamma(\sum\limits_{i=1}V\eta_i)}{\prod_{i=1}V\Gamma(\eta_i)}\prod_{i=1}V\beta_{i}{\eta_i-1})] \ & = Klog\Gamma(\sum\limits_{i=1}V\eta_i) - K\sum\limits_{i=1}Vlog\Gamma(\eta_i) + \sum\limits_{k=1}^KE_q[\sum\limits_{i=1}^V(\eta_i-1) log\beta_{ki}] \end{aligned}$$

第(15)式的第三项的期望部分，可以用上面讲到的指数分布族的性质，转化为一个求导过程。即：$$E_q[\sum\limits_{i=1}^Vlog\beta_{ki}] = (log\Gamma(\lambda_{ki} ) - log\Gamma(\sum\limits_{i{'}=1}V\lambda_{ki{'}})){'} = \Psi(\lambda_{ki}) - \Psi(\sum\limits_{i{'}=1}V\lambda_{ki^{'}})$$

其中：$$\Psi(x) = \frac{d}{d x}log\Gamma(x) = \frac{\Gamma^{'}(x)}{\Gamma(x)}$$

最终，我们得到EBLO第一项的展开式为：$$\begin{aligned} E_q[logp(\beta|\eta)] & = Klog\Gamma(\sum\limits_{i=1}V\eta_i) - K\sum\limits_{i=1}Vlog\Gamma(\eta_i) + \sum\limits_{k=1}K\sum\limits_{i=1}V(\eta_i-1)(\Psi(\lambda_{ki}) - \Psi(\sum\limits_{i{'}=1}V\lambda_{ki^{'}}) ) \end{aligned}$$

类似的方法求解其他6项，可以得到ELBO的最终关于变分参数$$\lambda,\phi, \gamma$$的表达式。其他6项的表达式为：

$$\begin{aligned} E_q[logp(z|\theta)] = \sum\limits_{n=1}N\sum\limits_{k=1}K\phi_{nk}\Psi(\gamma_{k}) - \Psi(\sum\limits_{k{'}=1}K\gamma_{k^{'}}) \end{aligned}$$

$$\begin{aligned} E_q[logp(\theta|\alpha)] & = log\Gamma(\sum\limits_{k=1}K\alpha_k) - \sum\limits_{k=1}Klog\Gamma(\alpha_k) + \sum\limits_{k=1}K(\alpha_k-1)(\Psi(\gamma_{k}) - \Psi(\sum\limits_{k{'}=1}K\gamma_{k{'}})) \end{aligned}$$

$$\begin{aligned} E_q[logp(w|z, \beta)] & = \sum\limits_{n=1}N\sum\limits_{k=1}K\sum\limits_{i=1}V\phi_{nk}w_ni(\Psi(\lambda_{ki}) - \Psi(\sum\limits_{i{'}=1}V\lambda_{ki^{'}}) ) \end{aligned}$$

$$\begin{aligned} E_q[logq(\beta|\lambda)] = \sum\limits_{k=1}K(log\Gamma(\sum\limits_{i=1}V\lambda_{ki}) - \sum\limits_{i=1}Vlog\Gamma(\lambda_{ki})) + \sum\limits_{k=1}K\sum\limits_{i=1}V (\lambda_{ki}-1)(\Psi(\lambda_{ki}) - \Psi(\sum\limits_{i{'}=1}V\lambda_{ki{'}}) )\end{aligned}$$

$$\begin{aligned} E_q[logq(z|\phi)] & = \sum\limits_{n=1}N\sum\limits_{k=1}K\phi_{nk}log\phi_{nk} \end{aligned}$$

$$\begin{aligned} E_q[logq(\theta|\gamma)] & = log\Gamma(\sum\limits_{k=1}K\gamma_k) - \sum\limits_{k=1}Klog\Gamma(\gamma_k) + \sum\limits_{k=1}K(\gamma_k-1)(\Psi(\gamma_{k}) - \Psi(\sum\limits_{k{'}=1}K\gamma_{k{'}}))\end{aligned}$$

有了ELBO的具体的关于变分参数$$\lambda,\phi, \gamma$$的表达式，我们就可以用EM算法来迭代更新变分参数和模型参数了。

4. EM算法之E步：获取最优变分参数

有了前面变分推断得到的ELBO函数为基础，我们就可以进行EM算法了。但是和EM算法不同的是这里的E步需要在包含期望的EBLO计算最佳的变分参数。如何求解最佳的变分参数呢？通过对ELBO函数对各个变分参数$$\lambda,\phi, \gamma$$分别求导并令偏导数为0，可以得到迭代表达式，多次迭代收敛后即为最佳变分参数。

这里就不详细推导了，直接给出各个变分参数的表达式如下：

$$\begin{aligned} \phi_{nk} & \propto exp(\sum\limits_{i=1}Vw_ni(\Psi(\lambda_{ki}) - \Psi(\sum\limits_{i{'}=1}V\lambda_{ki{'}}) ) + \Psi(\gamma_{k}) - \Psi(\sum\limits_{k{'}=1}K\gamma_{k{'}}))\end{aligned}$$

其中，$$w_n^i =1$$当且仅当文档中第n个词为词汇表中第i个词。

$$\begin{aligned} \gamma_k & = \alpha_k + \sum\limits_{n=1}^N\phi_{nk} \end{aligned}$$

$$\begin{aligned} \lambda_{ki} & = \eta_i + \sum\limits_{n=1}N\phi_{nk}w_ni \end{aligned}$$

由于变分参数$$\lambda$$决定了$$\beta$$的分布，对于整个语料是共有的，因此我们有：

$$\begin{aligned} \lambda_{ki} & = \eta_i + \sum\limits_{d=1}M\sum\limits_{n=1}{N_d}\phi_{dnk}w_{dn}^i \end{aligned}$$

最终我们的E步就是用（23）（24）（26）式来更新三个变分参数。当我们得到三个变分参数后，不断循环迭代更新，直到这三个变分参数收敛。当变分参数收敛后，下一步就是M步，固定变分参数，更新模型参数$$\alpha,\eta$$了。

5. EM算法之M步：更新模型参数

由于我们在E步，已经得到了当前最佳变分参数，现在我们在M步就来固定变分参数，极大化ELBO得到最优的模型参数$$\alpha,\eta$$。求解最优的模型参数$$\alpha,\eta$$的方法有很多，梯度下降法，牛顿法都可以。LDA这里一般使用的是牛顿法，即通过求出ELBO对于$$\alpha,\eta$$的一阶导数和二阶导数的表达式，然后迭代求解$$\alpha,\eta$$在M步的最优解。

对于$$\alpha$$,它的一阶导数和二阶导数的表达式为：

$$\nabla_{\alpha_k}L = M(\Psi(\sum\limits_{k{'}=1}K\alpha_{k{'}}) - \Psi(\alpha_{k}) ) + \sum\limits_{d=1}M(\Psi{'}(\gamma_{dk}) - \Psi{'}(\sum\limits_{k{'}=1}K\gamma_{dk^{'}}))$$

$$\nabla_{\alpha_k\alpha_j}L = M(\Psi{'}(\sum\limits_{k{'}=1}K\alpha_{k{'}})- \delta(k,j)\Psi^{'}(\alpha_{k}) )$$

其中，当且仅当k=j时，$$\delta(k,j)=1$$,否则$$\delta(k,j)=0$$。

对于$$\eta$$,它的一阶导数和二阶导数的表达式为：

$$\nabla_{\eta_i}L = K(\Psi(\sum\limits_{i{'}=1}V\eta_{i{'}}) - \Psi(\eta_{i}) ) + \sum\limits_{k=1}K(\Psi{'}(\lambda_{ki}) - \Psi{'}(\sum\limits_{i{'}=1}V\lambda_{ki^{'}}))$$

$$\nabla_{\eta_i\eta_j}L = K(\Psi{'}(\sum\limits_{i{'}=1}V\eta_{i{'}}) - \delta(i,j)\Psi^{'}(\eta_{i}) )$$

其中，当且仅当i=j时，$$\delta(i,j)=1$$,否则$$\delta(i,j)=0$$。

最终牛顿法法迭代公式为：

$$\begin{aligned} \alpha_{k+1} = \alpha_k + \frac{\nabla_{\alpha_k}L}{\nabla_{\alpha_k\alpha_j}L} \end{aligned}$$

$$\begin{aligned} \eta_{i+1} = \eta_i+ \frac{\nabla_{\eta_i}L}{\nabla_{\eta_i\eta_j}L} \end{aligned}$$

6. LDA变分推断EM算法流程总结

下面总结下LDA变分推断EM的算法的概要流程。

输入：主题数K,M个文档与对应的词。

1） 初始化$$\alpha,\eta$$向量。

2）开始EM算法迭代循环直到收敛。

a) 初始化所有的$$\phi, \gamma, \lambda$$，进行LDA的E步迭代循环,直到$$\lambda,\phi, \gamma$$收敛。

(i) for d from 1 to M:

for n from 1 to $$N_d$$:

for k from 1 to K:

按照(23)式更新$$\phi_{nk}$$

标准化$$\phi_{nk}$$使该向量各项的和为1.

按照(24) 式更新$$\gamma_{k}$$。

(ii) for k from 1 to K:

for i from 1 to V:

按照(26) 式更新$$\lambda{ki}$$。

(iii)如果$$\phi, \gamma, \lambda$$均已收敛，则跳出a)步，否则回到(i)步。

b) 进行LDA的M步迭代循环， 直到$$\alpha,\eta$$收敛

(i) 按照(27)(28)式用牛顿法迭代更新$$\alpha,\eta$$直到收敛

c) 如果所有的参数均收敛，则算法结束，否则回到第2)步。

算法结束后，我们可以得到模型的后验参数$$\alpha,\eta$$,以及我们需要的近似模型主题词分布$$\lambda$$,以及近似训练文档主题分布$$\gamma$$。