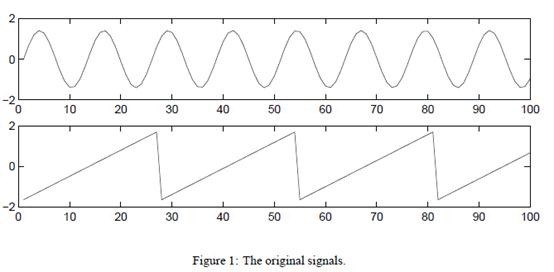
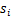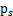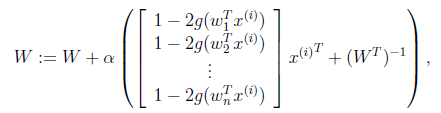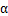在高维数据处理中，为了简化计算量以及储存空间，需要对这些高维数据进行一定程度上的降维，并尽量保证数据的不失真。PCA和ICA是两种常用的降维方法。
PCA：principal component analysis ，主成分分析
ICA ：Independent component analysis，独立成分分析
PCA,ICA都是统计理论当中的概念，在机器学习当中应用很广，比如图像，语音，通信的分析处理。
从线性代数的角度去理解，PCA和ICA都是要找到一组基，这组基张成一个特征空间，数据的处理就都需要映射到新空间中去。
两者常用于机器学习中提取特征后的降维操作
ICA是找出构成信号的相互独立部分(不需要正交)，对应高阶统计量分析。ICA理论认为用来观测的混合数据阵X是由独立元S经过A线性加权获得。ICA理论的目标就是通过X求得一个分离矩阵W，使得W作用在X上所获得的信号Y是独立源S的最优逼近，该关系可以通过下式表示：
Y = WX = WAS ， A = inv(W)
ICA相比与PCA更能刻画变量的随机统计特性，且能抑制高斯噪声。
1. 问题：
1、PCA是一种数据降维的方法，但是只对符合高斯分布的样本点比较有效，那么对于其他分布的样本，有没有主元分解的方法呢？
2、经典的鸡尾酒宴会问题（cocktail party problem）。假设在party中有n个人，他们可以同时说话，我们也在房间中一些角落里共放置了n个声音接收器（Microphone）用来记录声音。宴会过后，我们从n个麦克风中得到了一组数据$$x{(i)}(x_1{(i)},x_2{(i)},....x_n{(i)});i=1,...,m$$，i表示采样的时间顺序，也就是说共得到了m组采样，每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
将第二个问题细化一下，有n个信号源$$s(s_1,s_2,....,s_n)T,;s \in Rn$$，每一维都是一个人的声音信号，每个人发出的声音信号独立。A是一个未知的混合矩阵（mixing matrix），用来组合叠加信号s，那么
$$x = As$$
x的意义在上文解释过，这里的x不是一个向量，是一个矩阵。其中每个列向量是$$x{(i)}$$，$$x{(i)}=As^{(i)}$$
表示成图就是
这张图来自
$$x{(i)}$$的每个分量都由$$s{(i)}$$的分量线性表示。A和s都是未知的，x是已知的，我们要想办法根据x来推出s。这个过程也称作为盲信号分离。
令$$W=A{-1}$$，那么$$s{(i)}=A{-1}x{(i)}=Wx^{(i)}$$
将W表示成
$$W=\begin{bmatrix} ...w_1^T...\ .......\
...w_n^T...\end{bmatrix}$$
其中$$w_i \in R^n$$，其实就是将$$w_i$$写成行向量形式。那么得到：
$$s_j{(i)}=w_jTx^{(i)}$$
2. ICA的不确定性（ICA ambiguities）
由于w和s都不确定，那么在没有先验知识的情况下，无法同时确定这两个相关参数。比如上面的公式s=wx。当w扩大两倍时，s只需要同时扩大两倍即可，等式仍然满足，因此无法得到唯一的s。同时如果将人的编号打乱，变成另外一个顺序，如上图的蓝色节点的编号变为3,2,1，那么只需要调换A的列向量顺序即可，因此也无法单独确定s。这两种情况称为原信号不确定。
还有一种ICA不适用的情况，那就是信号不能是高斯分布的。假设只有两个人发出的声音信号符合多值正态分布, $$s\sim N(0, I)$$，I是2*2的单位矩阵，s的概率密度函数就不用说了吧，以均值0为中心，投影面是椭圆的山峰状（参见多值高斯分布）。因为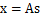
，因此，x也是高斯分布的，均值为0，协方差为$$E[xx^T]=E[AssTAT]=AA^T$$。
令R是正交阵$$RRT=RTR=I$$, $$A{'}=AR$$。如果将A替换成A’。那么$$x{'}=A{'}s$$。s分布没变，因此x’仍然是均值为0，协方差$$E[x{'}(x{'})^T]=E[A{'}ssT(A{'})T]=E[ARssT(AR)T]=ARRTAT=AAT$$。
因此，不管混合矩阵是A还是A’，x的分布情况是一样的，那么就无法确定混合矩阵，也就无法确定原信号。
3. 密度函数和线性变换
在讨论ICA具体算法之前，我们先来回顾一下概率和线性代数里的知识。
假设我们的随机变量s有概率密度函数$$P_s(s)$$（连续值是概率密度函数，离散值是概率）。为了简单，我们再假设s是实数，还有一个随机变量x=As，A和x都是实数。令$$P_x$$是x的概率密度，那么怎么求$$P_x$$？
令$$W=A^{-1}$$，首先将式子变换成$$s=Wx$$，然后得到$$p_x(x)=p_s(Ws)$$，求解完毕。可惜这种方法是错误的。比如s符合均匀分布的话（$$s \sim Uniform[0,1]$$），那么s的概率密度是$$p_s(s)=1 {0<=s<=1}$$，现在令A=2，即x=2s，也就是说x在[0,2]上均匀分布，可知$$p_x(x)=0.5$$。然而，前面的推导会得到$$p_x(x)=p_s(0.5s)=1$$。正确的公式应该是
$$p_x(x)=p_s(Ws)|W|$$
推导方法f
$$F_x(x)=P(X<=x)=P(AS<=x)=P(S<=Wx)=F_s(Wx)$$
$$p_x(x)=F_x{'}(x)=F_s{,}(Wx)=p_s(Wx)|W|$$
更一般地，如果s是向量，A可逆的方阵，那么上式子仍然成立。
4. ICA算法
ICA算法归功于Bell和Sejnowski，这里使用最大似然估计来解释算法，原始的论文中使用的是一个复杂的方法Infomax principal。
$$p(s)=\prod_{i=1}^{n}p_s(s_i)$$
这个公式代表一个假设前提：每个人发出的声音信号各自独立。有了p(s)，我们可以求得p(x)
$$p(x)=p_s(Wx)|W|=|W|\prod_{i=1}{n}p_s(w_iTx)$$
左边是每个采样信号x（n维向量）的概率，右边是每个原信号概率的乘积的|W|倍。
前面提到过，如果没有先验知识，我们无法求得W和s。因此我们需要知道$$p_s(s_i)$$，我们打算选取一个概率密度函数赋给s，但是我们不能选取高斯分布的密度函数。在概率论里我们知道密度函数p(x)由累计分布函数（cdf）F(x)求导得到。F(x)要满足两个性质是：单调递增和在[0,1]。我们发现sigmoid函数很适合，定义域负无穷到正无穷，值域0到1，缓慢递增。我们假定s的累积分布函数符合sigmoid函数
$$g(s)= \frac {1} {1+e^{-s}}$$
求导后
$$p_s(s)=g{'}(s)=\frac {es} {(1+es)2}$$
这就是s的密度函数。这里s是实数。
如果我们预先知道s的分布函数，那就不用假设了，但是在缺失的情况下，sigmoid函数能够在大多数问题上取得不错的效果。由于上式中$$p_s(s)$$是个对称函数，因此E[s]=0（s的均值为0），那么E[x]=E[As]=0，x的均值也是0。
知道了$$p_s(s)$$，就剩下W了。给定采样后的训练样本$$x{(i)}(x_1{(i)},x_2{(i)},....x_n{(i)});i=1,...,m$$，样本对数似然估计如下：
使用前面得到的x的概率密度函数，得
$$l(W)=\sum_{i=1}{m}(\sum_{j=1}{n}log ;g{'}(w_jTx^{(i)})+log|W|)$$
大括号里面是$$p(x^{(i)})$$。
接下来就是对W求导了，这里牵涉一个问题是对行列式|W|进行求导的方法，属于矩阵微积分。这里先给出结果，在文章最后再给出推导公式。
$$\bigtriangledown _w|W|=|W|(W{-1})T$$
最终得到的求导后公式如下，$$logg^{'}(s)$$的导数为$$1-2g(s)$$（可以自己验证）：
当迭代求出W后，便可得到$$s{(i)}=Wx{(i)}$$来还原出原始信号。
**注意：**我们计算最大似然估计时，假设了$$x{(i)}$$与$$y{(i)}$$之间是独立的，然而对于语音信号或者其他具有时间连续依赖特性（比如温度）上，这个假设不能成立。但是在数据足够多时，假设独立对效果影响不大，同时如果事先打乱样例，并运行随机梯度上升算法，那么能够加快收敛速度。
回顾一下鸡尾酒宴会问题，s是人发出的信号，是连续值，不同时间点的s不同，每个人发出的信号之间独立（$$s_i$$和$$s_j$$之间独立）。s的累计概率分布函数是sigmoid函数，但是所有人发出声音信号都符合这个分布。A（W的逆阵）代表了s相对于x的位置变化，x是s和A变化后的结果。
5. 实例
s=2时的原始信号
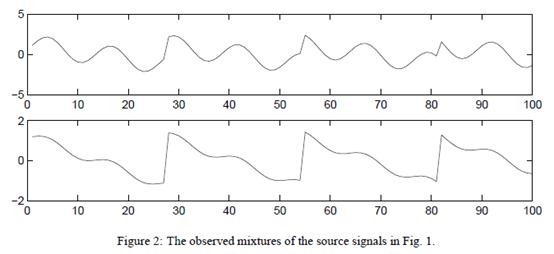
观察到的x信号
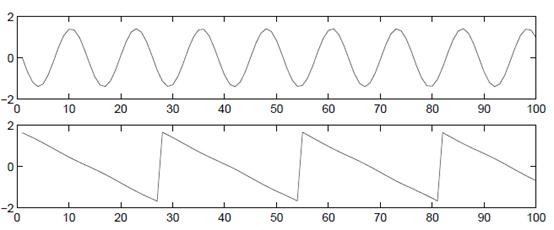
使用ICA还原后的s信号
6. 行列式的梯度
对行列式求导，设矩阵A是n×n的，我们知道行列式与代数余子式有关，
$$|A|=\sum_{i=1}{n}(-1){i+j}A_{ij}|A_{ij}| (for ;; any ;;j \in 1,...n)$$
$$A_{ij}$$是去掉第i行第j列后的余子式，那么对$$A_{kl}$$求导得
$$\frac{\partial }{\partial A_{kl}}|A|=\frac{\partial }{\partial A_{kl}}\sum_{i=1}{n}(-1){i+j}A_{ij}|A_{ij}=(-1)^{k+l}|A_{kl}|=(adj(A))_{lk}$$
adj(A)跟我们线性代数中学的$$A^{*}$$是一个意思，因此
$$\triangledown_A|A|=(adj(A))T=|A|A{-T}$$
