SMO算法原理
1. 回顾SVM优化目标函数
我们首先回顾下我们的优化目标函数:
$$ min(\alpha);; \frac{1}{2}\sum\limits_{i=1,j=1}{m}\alpha_i\alpha_jy_iy_jK(x_i,x_j) - \sum\limits_{i=1}{m}\alpha_i $$
$$ s.t. ; \sum\limits_{i=1}^{m}\alpha_iy_i = 0 $$
$$ 0 \leq \alpha_i \leq C $$
我们的解要满足的KKT条件的对偶互补条件为:$$\alpha_{i}{*}(y_i(w{} \bullet \phi(x_i) + b^{}) - 1) = 0$$
根据这个KKT条件的对偶互补条件,我们有:
$$ \alpha_{i}{*} = 0 \Rightarrow y_i(w{*} \bullet \phi(x_i) + b) \geq 1 $$
$$ 0 \leq \alpha_{i}{*} \leq C \Rightarrow y_i(w{*} \bullet \phi(x_i) + b) = 1 $$
$$ \alpha_{i}{*}= C \Rightarrow y_i(w{*} \bullet \phi(x_i) + b) \leq 1 $$
由于$$w{*} = \sum\limits_{j=1}{m}\alpha_j{*}y_j\phi(x_j)$$,我们令$$g(x) = w{} \bullet \phi(x) + b =\sum\limits_{j=1}{m}\alpha_j{}y_jK(x, x_j)+ b^{*}$$,则有:
$$ \alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i) \geq 1 $$
$$ 0 \leq \alpha_{i}^{*} \leq C \Rightarrow y_ig(x_i) = 1 $$
$$ \alpha_{i}^{*}= C \Rightarrow y_ig(x_i) \leq 1 $$
2. SMO算法的基本思想
上面这个优化式子比较复杂,里面有m个变量组成的向量$$\alpha$$需要在目标函数极小化的时候求出。直接优化时很难的。SMO算法则采用了一种启发式的方法。它每次只优化两个变量,将其他的变量都视为常数。由于$$\sum\limits_{i=1}^{m}\alpha_iy_i = 0$$.假如将$$\alpha_3, \alpha_4, ..., \alpha_m$$ 固定,那么$$\alpha_1, \alpha_2$$之间的关系也确定了。这样SMO算法将一个复杂的优化算法转化为一个比较简单的两变量优化问题。
为了后面表示方便,我们定义$$K_{ij} = \phi(x_i) \bullet \phi(x_j)$$
由于$$\alpha_3, \alpha_4, ..., \alpha_m$$都成了常量,所有的常量我们都从目标函数去除,这样我们上一节的目标优化函数变成下式:
$$ min(\alpha_1, \alpha_1);; \frac{1}{2}K_{11}\alpha_12 + \frac{1}{2}K_{22}\alpha_22 +y_1y_2K_{12}\alpha_1 \alpha_2 -(\alpha_1 + \alpha_2) +y_1\alpha_1\sum\limits_{i=3}{m}y_i\alpha_iK_{i1} + y_2\alpha_2\sum\limits_{i=3}{m}y_i\alpha_iK_{i2} $$
$$ s.t. ;;\alpha_1y_1 + \alpha_2y_2 = -\sum\limits_{i=3}^{m}y_i\alpha_i = \varsigma $$
$$ 0 \leq \alpha_i \leq C ;; i =1,2 $$
3. SMO算法目标函数的优化
为了求解上面含有这两个变量的目标优化问题,我们首先分析约束条件,所有的$$\alpha_1, \alpha_2$$都要满足约束条件,然后在约束条件下求最小。
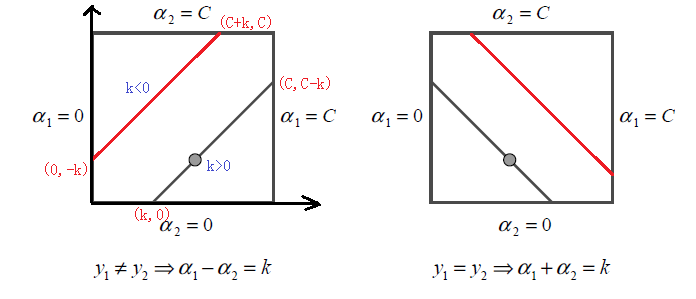
根据上面的约束条件$$\alpha_1y_1 + \alpha_2y_2 = \varsigma;;0 \leq \alpha_i \leq C ;; i =1,2$$,又由于$$y_1,y_2$$均只能取值1或者-1, 这样$$\alpha_1, \alpha_2$$在[0,C]和[0,C]形成的盒子里面,并且两者的关系直线的斜率只能为1或者-1,也就是说$$\alpha_1, \alpha_2$$的关系直线平行于[0,C]和[0,C]形成的盒子的对角线,如下图所示:
由于$$\alpha_1, \alpha_2$$的关系被限制在盒子里的一条线段上,所以两变量的优化问题实际上仅仅是一个变量的优化问题。不妨我们假设最终是$$\alpha_2$$的优化问题。由于我们采用的是启发式的迭代法,假设我们上一轮迭代得到的解是$$\alpha_1{old}, \alpha_2{old}$$,假设沿着约束方向$$\alpha_2$$未经剪辑的解是$$\alpha_2{new,unc}$$.本轮迭代完成后的解为$$\alpha_1{new}, \alpha_2^{new}$$
由于$$\alpha_2{new}$$必须满足上图中的线段约束。假设L和H分别是上图中$$\alpha_2{new}$$所在的线段的边界。那么很显然我们有:$$L \leq \alpha_2^{new} \leq H$$
而对于L和H,我们也有限制条件如果是上面左图中的情况,则
$$ L = max(0, \alpha_2{old}-\alpha_1{old}) ;;;H = min(C, C+\alpha_2{old}-\alpha_1{old}) $$
如果是上面右图中的情况,我们有:
$$ L = max(0, \alpha_2{old}+\alpha_1{old}-C) ;;; H = min(C, \alpha_2{old}+\alpha_1{old}) $$
也就是说,假如我们通过求导得到的$$\alpha_2{new,unc}$$,则最终的$$\alpha_2{new}$$应该为:
$$\alpha_2{new}= \begin{cases} H& {L \leq \alpha_2{new,unc} > H}\ \alpha_2{new,unc}& {L \leq \alpha_2{new,unc} \leq H}\ L& {\alpha_2^{new,unc} < L} \end{cases}$$
那么如何求出$$\alpha_2^{new,unc}$$呢?很简单,我们只需要将目标函数对$$\alpha_2$$求偏导数即可。
首先我们整理下我们的目标函数。
为了简化叙述,我们令$$E_i = g(x_i)-y_i = \sum\limits_{j=1}{m}\alpha_j{*}y_jK(x_i, x_j)+ b - y_i$$,
其中g(x)就是我们在第一节里面的提到的$$g(x) = w{*} \bullet \phi(x) + b =\sum\limits_{j=1}{m}\alpha_j{*}y_jK(x, x_j)+ b{*}$$
我们令$$v_i = \sum\limits_{i=3}{m}y_j\alpha_jK(x_i,x_j) = g(x_i) - \sum\limits_{i=1}{2}y_j\alpha_jK(x_i,x_j) -b$$
这样我们的优化目标函数进一步简化为:$$W(\alpha_1,\alpha_2) = \frac{1}{2}K_{11}\alpha_12 + \frac{1}{2}K_{22}\alpha_22 +y_1y_2K_{12}\alpha_1 \alpha_2 -(\alpha_1 + \alpha_2) +y_1\alpha_1v_1 + y_2\alpha_2v_2$$
由于$$\alpha_1y_1 + \alpha_2y_2 = \varsigma$$,并且$$y_i^2 = 1$$,可以得到$$\alpha_1$$用$$\alpha_2$$表达的式子为:$$\alpha_1 = y_1(\varsigma - \alpha_2y_2)$$
将上式带入我们的目标优化函数,就可以消除$$\alpha_1$$,得到仅仅包含$$\alpha_2$$的式子。$$W(\alpha_2) = \frac{1}{2}K_{11}(\varsigma - \alpha_2y_2)2 + \frac{1}{2}K_{22}\alpha_22 +y_2K_{12}(\varsigma - \alpha_2y_2) \alpha_2 -(\alpha_1 + \alpha_2) +(\varsigma - \alpha_2y_2)v_1 + y_2\alpha_2v_2$$
忙了半天,我们终于可以开始求$$\alpha_2{new,unc}$$了,现在我们开始通过求偏导数来得到$$\alpha_2{new,unc}$$。
$$\frac{\partial W}{\partial \alpha2} = K{11}\alpha2 + K{22}\alpha2 -2K{12}\alpha2 - K{11}\varsigma y2 + K{12}\varsigma y_2 +y_1y_2 -1 -v_1y_2 +y_2v_2 = 0$$
整理上式有:$$( K{11} +K{22}-2K{12})\alpha_2 = y_2(y_2-y_1 + \varsigma K{11} - \varsigma K_{12} + v_1 - v_2) $$
$$= y_2(y_2-y_1 + \varsigma K_{11} - \varsigma K_{12} + (g(x_1) - \sum\limits_{j=1}{2}y_j\alpha_jK_{1j} -b ) -(g(x_2) - \sum\limits_{j=1}{2}y_j\alpha_jK_{2j} -b))$$
将$$\varsigma = \alpha_1y_1 + \alpha_2y_2$$带入上式,我们有:
$$(K_{11} +K_{22}-2K_{12})\alpha_2{new,unc} = y_2((K_{11} +K_{22}-2K_{12})\alpha_2{old}y_2 +y_2-y_1 +g(x_1) - g(x_2))$$
$$;;;; = (K_{11} +K_{22}-2K_{12}) \alpha_2^{old} + y2(E_1-E_2)$$
我们终于得到了$$\alpha_2{new,unc}$$的表达式:$$\alpha_2{new,unc} = \alpha_2^{old} + \frac{y2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
利用上面讲到的$$\alpha_2{new,unc}$$和$$\alpha_2{new}$$的关系式,我们就可以得到我们新的$$\alpha_2{new}$$了。利用$$\alpha_2{new}$$和$$\alpha_1{new}$$的线性关系,我们也可以得到新的$$\alpha_1{new}$$。
4. SMO算法两个变量的选择
SMO算法需要选择合适的两个变量做迭代,其余的变量做常量来进行优化,那么怎么选择这两个变量呢?
4.1 第一个变量的选择
SMO算法称选择第一个变量为外层循环,这个变量需要选择在训练集中违反KKT条件最严重的样本点。对于每个样本点,要满足的KKT条件我们在第一节已经讲到了:
$$ \alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i) \geq 1 $$
$$ 0 \leq \alpha_{i}^{*} \leq C \Rightarrow y_ig(x_i) =1 $$
$$ \alpha_{i}^{*}= C \Rightarrow y_ig(x_i) \leq 1 $$
一般来说,我们首先选择违反$$0 \leq \alpha_{i}{*} \leq C \Rightarrow y_ig(x_i) =1$$这个条件的点。如果这些支持向量都满足KKT条件,再选择违反$$\alpha_{i}{} = 0 \Rightarrow y_ig(x_i) \geq 1 $$和$$\alpha_{i}^{}= C \Rightarrow y_ig(x_i) \leq 1$$的点。
4.2 第二个变量的选择
SMO算法称选择第二个变量为内层循环,假设我们在外层循环已经找到了$$\alpha_1$$, 第二个变量$$\alpha_2$$的选择标准是让|E1-E2|有足够大的变化。由于$$\alpha_1$$定了的时候,$$E_1$$也确定了,所以要想|E1-E2|最大,只需要在$$E_1$$为正时,选择最小的$$E_i$$作为$$E_2$$, 在$$E_1$$为负时,选择最大的$$E_i$$作为$$E_2$$,可以将所有的$$E_i$$保存下来加快迭代。
如果内存循环找到的点不能让目标函数有足够的下降, 可以采用遍历支持向量点来做$$\alpha_2$$,直到目标函数有足够的下降, 如果所有的支持向量做$$\alpha_2$$都不能让目标函数有足够的下降,可以跳出循环,重新选择$$\alpha_1$$
4.3 计算阈值b和差值E_i
在每次完成两个变量的优化之后,需要重新计算阈值b。当$$0 \leq \alpha_{1}{new} \leq C$$时,我们有$$y_1 - \sum\limits_{i=1}{m}\alpha_iy_iK_{i1} -b_1 = 0$$
于是新的$$b_1{new}$$为:$$b_1{new} = y_1 - \sum\limits_{i=3}{m}\alpha_iy_iK_{i1} - \alpha_{1}{new}y_1K_{11} - \alpha_{2}^{new}y_2K_{21}$$
计算出$$E_1$$为:$$E_1 = g(x_1) - y_1 = \sum\limits_{i=3}{m}\alpha_iy_iK_{i1} + \alpha_{1}{old}y_1K_{11} + \alpha_{2}{old}y_2K_{21} + b{old} -y_1$$
可以看到上两式都有$$y_1 - \sum\limits_{i=3}{m}\alpha_iy_iK_{i1}$$,因此可以将$$b_1{new}$$用$$E_1$$表示为:$$b_1{new} = -E_1 -y_1K_{11}(\alpha_{1}{new} - \alpha_{1}{old}) -y_2K_{21}(\alpha_{2}{new} - \alpha_{2}{old}) + b{old}$$
同样的,如果$$0 \leq \alpha_{2}{new} \leq C$$, 那么有:$$b_2{new} = -E_2 -y_1K_{12}(\alpha_{1}{new} - \alpha_{1}{old}) -y_2K_{22}(\alpha_{2}{new} - \alpha_{2}{old}) + b^{old}$$
最终的$$b{new}$$为:$$b{new} = \frac{b_1{new} + b_2{new}}{2}$$
得到了$$b{new}$$我们需要更新$$E_i:E_i = \sum\limits_{S}y_j\alpha_jK(x_i,x_j) + b{new} -y_i$$
其中,S是所有支持向量$$x_j$$的集合。
好了,SMO算法基本讲完了,我们来归纳下SMO算法。
5. SMO算法总结
输入是m个样本$${(x_1,y_1), (x_2,y_2), ..., (x_m,y_m),}$$,其中x为n维特征向量。y为二元输出,值为1,或者-1.精度e。
输出是近似解\alpha
1)取初值$$\alpha^{0} = 0, k =0$$
2)按照4.1节的方法选择$$\alpha_1k$$,接着按照4.2节的方法选择$$\alpha_2k$$,求出新的$$\alpha_2{new,unc}$$。$$\alpha_2{new,unc} = \alpha_2^{k} + \frac{y_2(E_1-E_2)}{K_{11} +K_{22}-2K_{12})}$$
3)按照下式求出$$\alpha_2^{k+1}$$
$$\alpha_2{k+1}= \begin{cases} H& {L \leq \alpha_2{new,unc} > H}\ \alpha_2{new,unc}& {L \leq \alpha_2{new,unc} \leq H}\ L& {\alpha_2^{new,unc} < L} \end{cases}$$
4)利用$$\alpha_2{k+1}$$和$$\alpha_1{k+1}$$的关系求出$$\alpha_1^{k+1}$$
5)按照4.3节的方法计算$$b^{k+1}$$和$$E_i$$
6)在精度e范围内检查是否满足如下的终止条件:
$$ \sum\limits_{i=1}^{m}\alpha_iy_i = 0 $$
$$ 0 \leq \alpha_i \leq C, i =1,2...m $$
$$ \alpha_{i}^{k+1} = 0 \Rightarrow y_ig(x_i) \geq 1 $$
$$ 0 \leq \alpha_{i}^{k+1} \leq C \Rightarrow y_ig(x_i) = 1 $$
$$ \alpha_{i}^{k+1}= C \Rightarrow y_ig(x_i) \leq 1 $$
7)如果满足则结束,返回$$\alpha^{k+1}$$,否则转到步骤2)。