LDA基础
在前面我们讲到了基于矩阵分解的LSI和NMF主题模型,这里我们开始讨论被广泛使用的主题模型:隐含狄利克雷分布(Latent Dirichlet Allocation,以下简称LDA)。注意机器学习还有一个LDA,即线性判别分析,主要是用于降维和分类的,如果大家需要了解这个LDA的信息,参看之前写的线性判别分析LDA原理总结。文本关注于隐含狄利克雷分布对应的LDA。
1. LDA贝叶斯模型
LDA是基于贝叶斯模型的,涉及到贝叶斯模型离不开“先验分布”,“数据(似然)”和"后验分布"三块。在朴素贝叶斯算法原理小结中我们也已经讲到了这套贝叶斯理论。在贝叶斯学派这里:
先验分布 + 数据(似然)= 后验分布
这点其实很好理解,因为这符合我们人的思维方式,比如你对好人和坏人的认知,先验分布为:100个好人和100个的坏人,即你认为好人坏人各占一半,现在你被2个好人(数据)帮助了和1个坏人骗了,于是你得到了新的后验分布为:102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布,当你被1个好人(数据)帮助了和3个坏人(数据)骗了后,你又更新了你的后验分布为:103个好人和104个的坏人。依次继续更新下去。
2. 二项分布与Beta分布
对于上一节的贝叶斯模型和认知过程,假如用数学和概率的方式该如何表达呢?
对于我们的数据(似然),这个好办,用一个二项分布就可以搞定,即对于二项分布:$$Binom(k|n,p) = {n \choose k}pk(1-p){n-k}$$
其中p我们可以理解为好人的概率,k为好人的个数,n为好人坏人的总数。
虽然数据(似然)很好理解,但是对于先验分布,我们就要费一番脑筋了,为什么呢?因为我们希望这个先验分布和数据(似然)对应的二项分布集合后,得到的后验分布在后面还可以作为先验分布!就像上面例子里的“102个好人和101个的坏人”,它是前面一次贝叶斯推荐的后验分布,又是后一次贝叶斯推荐的先验分布。也即是说,我们希望先验分布和后验分布的形式应该是一样的,这样的分布我们一般叫共轭分布。在我们的例子里,我们希望找到和二项分布共轭的分布。
和二项分布共轭的分布其实就是Beta分布。Beta分布的表达式为:$$Beta(p|\alpha,\beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p{\alpha-1}(1-p){{\beta-1}}$$
其中$$\Gamma$$是$$Gamma$$函数,满足$$\Gamma(x) = (x-1)!$$
仔细观察Beta分布和二项分布,可以发现两者的密度函数很相似,区别仅仅在前面的归一化的阶乘项。那么它如何做到先验分布和后验分布的形式一样呢?后验分布$$P(p|n,k,\alpha,\beta)$$推导如下:
$$\begin{aligned} P(p|n,k,\alpha,\beta)& \propto P(k|n,p)P(p|\alpha,\beta) \ & = P(k|n,p)P(p|\alpha,\beta) \& =Binom(k|n,p) Beta(p|\alpha,\beta) \ &={n \choose k}pk(1-p){n-k} \times \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p{\alpha-1}(1-p){{\beta-1}} \& \propto p{k+\alpha-1}(1-p){n-k + \beta -1}\end{aligned}$$
将上面最后的式子归一化以后,得到我们的后验概率为:$$P(p|n,k,\alpha,\beta) = \frac{\Gamma(\alpha + \beta + n)}{\Gamma(\alpha + k)\Gamma(\beta + n - k)}p{k+\alpha-1}(1-p){n-k + \beta -1}$$
可见我们的后验分布的确是Beta分布,而且我们发现:$$Beta(p|\alpha,\beta) + BinomCount(k,n-k) =Beta(p|\alpha + k,\beta +n-k)$$
这个式子完全符合我们在上一节好人坏人例子里的情况,我们的认知会把数据里的好人坏人数分别加到我们的先验分布上,得到后验分布。
我们在来看看Beta分布$$Beta(p|\alpha,\beta)$$的期望:$$\begin{aligned} E(Beta(p|\alpha,\beta)) & = \int_{0}{1}tBeta(p|\alpha,\beta)dt \& = \int_{0}{1}t\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}t{\alpha-1}(1-t){{\beta-1}}dt \& =\int_{0}{1}\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}t{\alpha}(1-t)^{{\beta-1}}dt\end{aligned}$$
由于上式最右边的乘积对应Beta分布$$Beta(p|\alpha+1,\beta),$$因此有:$$\int_{0}{1}\frac{\Gamma(\alpha + \beta+1)}{\Gamma(\alpha+1)\Gamma(\beta)}p{\alpha}(1-p)^{{\beta-1}} =1$$
这样我们的期望可以表达为:$$E(Beta(p|\alpha,\beta)) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha + \beta+1)} = \frac{\alpha}{\alpha + \beta}$$
这个结果也很符合我们的思维方式。
3. 多项分布与Dirichlet 分布
现在我们回到上面好人坏人的问题,假如我们发现有第三类人,不好不坏的人,这时候我们如何用贝叶斯来表达这个模型分布呢?之前我们是二维分布,现在是三维分布。由于二维我们使用了Beta分布和二项分布来表达这个模型,则在三维时,以此类推,我们可以用三维的Beta分布来表达先验后验分布,三项的多项分布来表达数据(似然)。
三项的多项分布好表达,我们假设数据中的第一类有$$m_1$$个好人,第二类有$$m_2$$个坏人,第三类为$$m_3 = n-m_1-m_2$$个不好不坏的人,对应的概率分别为$$p_1,p_2,p_3 = 1-p_1-p_2$$,则对应的多项分布为:$$multi(m_1,m_2,m_3|n,p_1,p_2,p_3) = \frac{n!}{m_1! m_2!m_3!}p_1{m_1}p_2{m_2}p_3^{m_3}$$
那三维的Beta分布呢?超过二维的Beta分布我们一般称之为狄利克雷(以下称为Dirichlet )分布。也可以说Beta分布是Dirichlet 分布在二维时的特殊形式。从二维的Beta分布表达式,我们很容易写出三维的Dirichlet分布如下:$$Dirichlet(p_1,p_2,p_3|\alpha_1,\alpha_2, \alpha_3) = \frac{\Gamma(\alpha_1+ \alpha_2 + \alpha_3)}{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}p_1{\alpha_1-1}(p_2){\alpha_2-1}(p_3)^{\alpha_3-1}$$
同样的方法,我们可以写出4维,5维,。。。以及更高维的Dirichlet 分布的概率密度函数。为了简化表达式,我们用向量来表示概率和计数,这样多项分布可以表示为:$$Dirichlet(\vec p| \vec \alpha)$$,而多项分布可以表示为:$$multi(\vec m| n, \vec p)$$。
一般意义上的K维Dirichlet 分布表达式为:$$Dirichlet(\vec p| \vec \alpha) = \frac{\Gamma(\sum\limits_{k=1}K\alpha_k)}{\prod_{k=1}K\Gamma(\alpha_k)}\prod_{k=1}Kp_k{\alpha_k-1}$$
而多项分布和Dirichlet 分布也满足共轭关系,这样我们可以得到和上一节类似的结论:$$Dirichlet(\vec p|\vec \alpha) + MultiCount(\vec m) =Dirichlet(\vec p|\vec \alpha + \vec m)$$
对于Dirichlet 分布的期望,也有和Beta分布类似的性质:$$E(Dirichlet(\vec p|\vec \alpha)) = (\frac{\alpha_1}{\sum\limits_{k=1}K\alpha_k}, \frac{\alpha_2}{\sum\limits_{k=1}K\alpha_k},...,\frac{\alpha_K}{\sum\limits_{k=1}^K\alpha_k})$$
4. LDA主题模型
前面做了这么多的铺垫,我们终于可以开始LDA主题模型了。
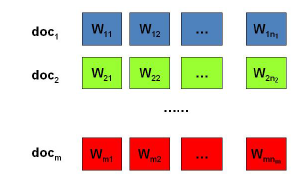
我们的问题是这样的,我们有M篇文档,对应第d个文档中有有$$N_d$$个词。即输入为如下图:
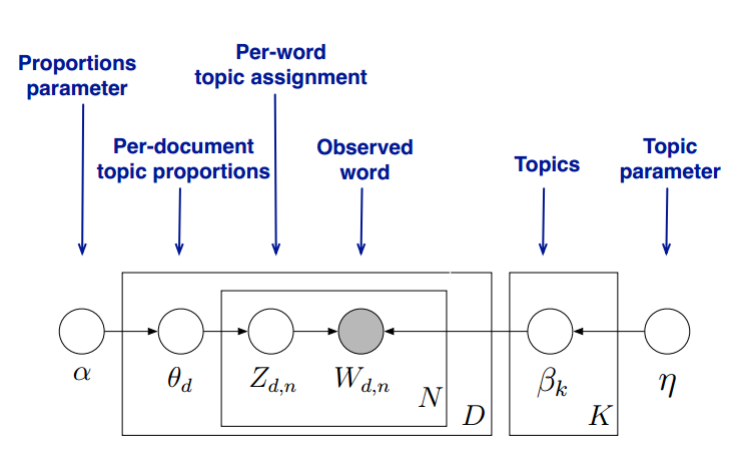
我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。在LDA模型中,我们需要先假定一个主题数目K,这样所有的分布就都基于K个主题展开。那么具体LDA模型是怎么样的呢?具体如下图:
LDA假设文档主题的先验分布是Dirichlet分布,即对于任一文档d, 其主题分布$$\theta_d$$为:$$\theta_d =Dirichlet(\vec \alpha)$$
其中,$$\alpha$$为分布的超参数,是一个K维向量。
LDA假设主题中词的先验分布是Dirichlet分布,即对于任一主题k, 其词分布$$\beta_k$$为:$$\beta_k=Dirichlet(\vec \eta)$$
其中,$$\eta$$为分布的超参数,是一个V维向量。V代表词汇表里所有词的个数。
对于数据中任一一篇文档d中的第n个词,我们可以从主题分布$$\theta_d$$中得到它的主题编号$$z_{dn}$$的分布为:$$z_{dn} = multi(\theta_d)$$
而对于该主题编号,得到我们看到的词$$w_{dn}$$的概率分布为:$$w_{dn} = multi(\beta_{z_{dn}})$$
理解LDA主题模型的主要任务就是理解上面的这个模型。这个模型里,我们有M个文档主题的Dirichlet分布,而对应的数据有M个主题编号的多项分布,这样$$(\alpha \to \theta_d \to \vec z_{d})$$就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。
如果在第d个文档中,第k个主题的词的个数为:$$n_d{(k)}$$, 则对应的多项分布的计数可以表示为$$\vec n_d = (n_d{(1)}, n_d{(2)},...n_d{(K)})$$
利用Dirichlet-multi共轭,得到$$\theta_d$$的后验分布为:$$Dirichlet(\theta_d | \vec \alpha +\vec n_d)$$
同样的道理,对于主题与词的分布,我们有K个主题与词的Dirichlet分布,而对应的数据有K个主题编号的多项分布,这样$$(\eta \to \beta_k \to \vec w_{(k)})$$就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。
如果在第k个主题中,第v个词的个数为:$$n_k{(v)}$$, 则对应的多项分布的计数可以表示为$$\vec n_k = (n_k{(1)}, n_k{(2)},...n_k{(V)})$$
利用Dirichlet-multi共轭,得到$$\beta_k$$的后验分布为:$$Dirichlet(\beta_k | \vec \eta+\vec n_k)$$
由于主题产生词不依赖具体某一个文档,因此文档主题分布和主题词分布是独立的。理解了上面这M+K组Dirichlet-multi共轭,就理解了LDA的基本原理了。
现在的问题是,基于这个LDA模型如何求解我们想要的每一篇文档的主题分布和每一个主题中词的分布呢?
一般有两种方法,第一种是基于Gibbs采样算法求解,第二种是基于变分推断EM算法求解。