线性支持回归

在前四篇里面我们讲到了SVM的线性分类和非线性分类，以及在分类时用到的算法。这些都关注与SVM的分类问题。实际上SVM也可以用于回归模型，本篇就对如何将SVM用于回归模型做一个总结。重点关注SVM分类和SVM回归的相同点与不同点。

1. SVM回归模型的损失函数度量

回顾下我们前面SVM分类模型中，我们的目标函数是让$$\frac{1}{2}||w||22$$最小，同时让各个训练集中的点尽量远离自己类别一边的的支持向量，即$$y_i(w \bullet \phi(x_i )+ b) \geq 1$$。如果是加入一个松弛变量$$\xi_i \geq 0$$,则目标函数是$$\frac{1}{2}||w||_22 +C\sum\limits{i=1}^{m}\xi_i$$,对应的约束条件变成：$$y_i(w \bullet \phi(x_i ) + b ) \geq 1 - \xi_i$$

但是我们现在是回归模型，优化目标函数可以继续和SVM分类模型保持一致为$$\frac{1}{2}||w||_2^2$$，但是约束条件呢？不可能是让各个训练集中的点尽量远离自己类别一边的的支持向量，因为我们是回归模型，没有类别。对于回归模型，我们的目标是让训练集中的每个点$$(x_i,y_i)$$,尽量拟合到一个线性模型$$y_i ~= w \bullet \phi(x_i ) +b$$。对于一般的回归模型，我们是用均方差作为损失函数,但是SVM不是这样定义损失函数的。

SVM需要我们定义一个常量$$\epsilon > 0$$,对于某一个点$$(x_i,y_i)$$，如果$$|y_i - w \bullet \phi(x_i ) -b| \leq \epsilon$$，则完全没有损失，如果$$|y_i - w \bullet \phi(x_i ) -b| > \epsilon$$,则对应的损失为$$|y_i - w \bullet \phi(x_i ) -b| - \epsilon$$，这个均方差损失函数不同，如果是均方差，那么只要$$y_i - w \bullet \phi(x_i ) -b \neq 0$$，那么就会有损失。

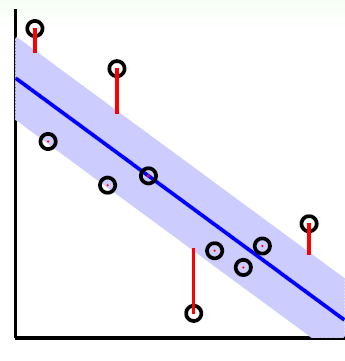
如下图所示，在蓝色条带里面的点都是没有损失的，但是外面的点的是有损失的，损失大小为红色线的长度。

总结下，我们的SVM回归模型的损失函数度量为：

$$err(x_i,y_i) = \begin{cases} 0 & {|y_i - w \bullet \phi(x_i ) -b| \leq \epsilon}\ |y_i - w \bullet \phi(x_i ) +b| - \epsilon & {|y_i - w \bullet \phi(x_i ) -b| > \epsilon} \end{cases}$$

2. SVM回归模型的目标函数的原始形式

上一节我们已经得到了我们的损失函数的度量，现在可以可以定义我们的目标函数如下：$$min;; \frac{1}{2}||w||_2^2 ;; s.t ;; |y_i - w \bullet \phi(x_i ) -b| \leq \epsilon (i =1,2,...m)$$

和SVM分类模型相似，回归模型也可以对每个样本$$(x_i,y_i)$$加入松弛变量$$\xi_i \geq 0$$, 但是由于我们这里用的是绝对值，实际上是两个不等式，也就是说两边都需要松弛变量，我们定义为$$\xi_i{\lor}, \xi_i{\land}$$, 则我们SVM回归模型的损失函数度量在加入松弛变量之后变为： $$ min;; \frac{1}{2}||w||2^2 + C\sum\limits{i=1}{m}(\xi_i{\lor}+ \xi_i{\land}) $$ $$ s.t. ;;; -\epsilon - \xi_i{\lor} \leq y_i - w \bullet \phi(x_i ) -b \leq \epsilon + \xi_i{\land} $$ $$ \xi_i{\lor} \geq 0,;; \xi_i^{\land} \geq 0 ;(i = 1,2,..., m) $$ 依然和SVM分类模型相似，我们可以用拉格朗日函数将目标优化函数变成无约束的形式，也就是拉格朗日函数的原始形式如下：

$$L(w,b,\alpha{\lor}, \alpha{\land}, \xi_i{\lor}, \xi_i{\land}, \mu{\lor}, \mu{\land}) = \frac{1}{2}||w||2^2 + C\sum\limits{i=1}{m}(\xi_i{\lor}+ \xi_i{\land}) + \sum\limits_{i=1}{m}\alpha{\lor}(-\epsilon - \xi_i{\lor} -y_i + w \bullet \phi(x_i) + b) + \sum\limits_{i=1}{m}\alpha{\land}(y_i - w \bullet \phi(x_i ) - b -\epsilon - \xi_i{\land}) - \sum\limits_{i=1}{m}\mu{\lor}\xi_i{\lor} - \sum\limits_{i=1}{m}\mu{\land}\xi_i^{\land}$$

其中$$\mu{\lor} \geq 0, \mu{\land} \geq 0, \alpha_i{\lor} \geq 0, \alpha_i{\land} \geq 0$$,均为拉格朗日系数。

3. SVM回归模型的目标函数的对偶形式

上一节我们讲到了SVM回归模型的目标函数的原始形式,我们的目标是$$min(w,b,\xi_i{\lor}, \xi_i{\land}); ;;;;;;;;max(\mu{\lor} \geq 0, \mu{\land} \geq 0, \alpha_i{\lor} \geq 0, \alpha_i{\land} \geq 0);L(w,b,\alpha{\lor}, \alpha{\land}, \xi_i{\lor}, \xi_i{\land}, \mu{\lor}, \mu{\land})$$

和SVM分类模型一样，这个优化目标也满足KKT条件，也就是说，我们可以通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解如下：$$max(\mu{\lor} \geq 0, \mu{\land} \geq 0, \alpha_i{\lor} \geq 0, \alpha_i{\land} \geq 0); ;;;;;;;;min(w,b,\xi_i{\lor}, \xi_i{\land});L(w,b,\alpha{\lor}, \alpha{\land}, \xi_i{\lor}, \xi_i{\land}, \mu{\lor}, \mu{\land})$$

我们可以先求优化函数对于w,b,$$\xi_i{\lor}, \xi_i{\land}$$的极小值, 接着再求拉格朗日乘子$$\alpha{\lor}, \alpha{\land}, \mu{\lor}, \mu{\land}$$的极大值。

首先我们来求优化函数对于w,b,$$\xi_i{\lor}, \xi_i{\land}$$的极小值，这个可以通过求偏导数求得： $$ \frac{\partial L}{\partial w} = 0 ;\Rightarrow w = \sum\limits_{i=1}{m}(\alpha_i{\land} - \alpha_i{\lor})\phi(x_i) $$ $$ \frac{\partial L}{\partial b} = 0 ;\Rightarrow \sum\limits_{i=1}{m}(\alpha_i{\land} - \alpha_i{\lor}) = 0 $$ $$ \frac{\partial L}{\partial \xi_i{\lor}} = 0 ;\Rightarrow C-\alpha{\lor}-\mu{\lor} = 0 $$ $$ \frac{\partial L}{\partial \xi_i{\land}} = 0 ;\Rightarrow C-\alpha{\land}-\mu{\land} = 0 $$ 好了，我们可以把上面4个式子带入$$L(w,b,\alpha{\lor}, \alpha{\land}, \xi_i{\lor}, \xi_i{\land}, \mu{\lor}, \mu{\land})$$去消去w,b$$,\xi_i{\lor}, \xi_i{\land}$$了。

看似很复杂，其实消除过程和系列第一篇第二篇文章类似，由于式子实在是冗长，这里我就不写出推导过程了，最终得到的对偶形式为： $$ max(\alpha{\lor}, \alpha{\land});; \sum\limits_{i=1}{m}(\epsilon-y_i)\alpha_i{\land}+ (\epsilon+y_i)\alpha_i{\lor}) - \frac{1}{2}\sum\limits_{i=1,j=1}{m}(\alpha_i{\land} - \alpha_i{\lor})(\alpha_j{\land} - \alpha_j{\lor})K_{ij} $$ $$ s.t. ; \sum\limits_{i=1}{m}(\alpha_i{\land} - \alpha_i{\lor}) = 0 $$ $$ 0 < \alpha_i{\lor} < C ; (i =1,2,...m) $$ $$ 0 < \alpha_i{\land} < C ; (i =1,2,...m) $$ 对目标函数取负号，求最小值可以得到和SVM分类模型类似的求极小值的目标函数如下： $$ min(\alpha{\lor}, \alpha{\land}); \frac{1}{2}\sum\limits_{i=1,j=1}{m}(\alpha_i{\land} - \alpha_i{\lor})(\alpha_j{\land} - \alpha_j{\lor})K_{ij} - \sum\limits_{i=1}{m}(\epsilon-y_i)\alpha_i{\land}+ (\epsilon+y_i)\alpha_i{\lor} $$ $$ s.t. ; \sum\limits_{i=1}{m}(\alpha_i{\land} - \alpha_i{\lor}) = 0 $$ $$ 0 < \alpha_i{\lor} < C ; (i =1,2,...m) $$ $$ 0 < \alpha_i{\land} < C ; (i =1,2,...m) $$ 对于这个目标函数，我们依然可以用第四篇讲到的SMO算法来求出对应的$$\alpha{\lor}, \alpha{\land}$$，进而求出我们的回归模型系数w, b。

4. SVM回归模型系数的稀疏性

在SVM分类模型中，我们的KKT条件的对偶互补条件为： $$\alpha_{i}{*}(y_i(w \bullet \phi(x_i) + b) - 1) = 0$$，而在回归模型中，我们的对偶互补条件类似如下： $$ \alpha_i{\lor}(\epsilon + \xi_i{\lor} + y_i - w \bullet \phi(x_i ) - b ) = 0 $$ $$ \alpha_i{\land}(\epsilon + \xi_i{\land} - y_i + w \bullet \phi(x_i ) + b ) = 0 $$ 根据松弛变量定义条件，如果$$|y_i - w \bullet \phi(x_i ) -b| < \epsilon$$，我们有$$\xi_i{\lor} = 0, \xi_i{\land}= 0$$，此时$$\epsilon + \xi_i{\lor} + y_i - w \bullet \phi(x_i ) - b \neq 0, \epsilon + \xi_i{\land} - y_i + w \bullet \phi(x_i ) + b \neq 0$$这样要满足对偶互补条件，只有$$\alpha_i{\lor} = 0, \alpha_i^{\land} = 0$$。

我们定义样本系数系数$$\beta_i =\alpha_i{\land}-\alpha_i{\lor}$$

根据上面w的计算式$$w = \sum\limits_{i=1}{m}(\alpha_i{\land} - \alpha_i{\lor})\phi(x_i)$$，我们发现此时$$\beta_i = 0$$,也就是说w不受这些在误差范围内的点的影响。对于在边界上或者在边界外的点，$$\alpha_i{\lor} \neq 0, \alpha_i^{\land} \neq 0$$，此时$$\beta_i \neq 0$$。

5. SVM 算法小结

这个系列终于写完了，这里按惯例SVM 算法做一个总结。SVM算法是一个很优秀的算法，在集成学习和神经网络之类的算法没有表现出优越性能前，SVM基本占据了分类模型的统治地位。目前则是在大数据时代的大样本背景下,SVM由于其在大样本时超级大的计算量，热度有所下降，但是仍然是一个常用的机器学习算法。

SVM算法的主要优点有：

1) 解决高维特征的分类问题和回归问题很有效,在特征维度大于样本数时依然有很好的效果。

2) 仅仅使用一部分支持向量来做超平面的决策，无需依赖全部数据。

3) 有大量的核函数可以使用，从而可以很灵活的来解决各种非线性的分类回归问题。

4)样本量不是海量数据的时候，分类准确率高，泛化能力强。

SVM算法的主要缺点有：

1) 如果特征维度远远大于样本数，则SVM表现一般。

2) SVM在样本量非常大，核函数映射维度非常高时，计算量过大，不太适合使用。

3）非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数。

4）SVM对缺失数据敏感。