2.9. 稀疏逆协方差
协方差矩阵的逆矩阵,通常称为精度矩阵(precision matrix),它与部分相关矩阵(partial correlation matrix)成正比。 它给出部分独立性关系。换句话说,如果两个特征在其他特征上有条件地独立, 则精度矩阵中的对应系数将为零。这就是为什么估计一个稀疏精度矩阵是有道理的: 通过从数据中学习独立关系,协方差矩阵的估计能更好处理。这被称为协方差选择。
在小样本的情况,即 n_samples 是数量级 n_features 或更小, 稀疏的逆协方差估计往往比收敛的协方差估计更好。 然而,在相反的情况下,或者对于非常相关的数据,它们可能在数值上不稳定。 此外,与收敛估算不同,稀疏估计器能够恢复非对角线结构 (off-diagonal structure)。
GraphLasso 估计器使用 L1 惩罚执行关于精度矩阵的稀疏性: alpha 参数越高,精度矩阵的稀疏性越大。 相应的 GraphLassoCV 对象使用交叉验证来自动设置 alpha 参数。
Note
结构恢复
从数据中的相关性恢复图形结构是一个具有挑战性的事情。如果您对这种恢复感兴趣,请记住:
- 相关矩阵的恢复比协方差矩阵更容易:在运行
GraphLasso前先标准化观察值 - 如果底层图具有比平均节点更多的连接节点,则算法将错过其中一些连接。
- 如果您的观察次数与底层图形中的边数相比不大,则不会恢复。
- 即使您具有良好的恢复条件,通过交叉验证(例如使用GraphLassoCV对象)选择的 Alpha 参数将导致选择太多边。 然而,相关边缘将具有比不相关边缘更重的权重。
数学公式如下:

其中: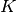 是要估计的精度矩阵(precision matrix),
是要估计的精度矩阵(precision matrix), 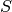 是样本的协方差矩阵。
是样本的协方差矩阵。 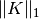 是非对角系数
是非对角系数 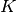 (off-diagonal coefficients)的绝对值之和。 用于解决这个问题的算法是来自 Friedman 2008 Biostatistics 论文的 GLasso 算法。 它与 R 语言
(off-diagonal coefficients)的绝对值之和。 用于解决这个问题的算法是来自 Friedman 2008 Biostatistics 论文的 GLasso 算法。 它与 R 语言 glasso 包中的算法相同。
例子:
合成数据示例,显示结构的一些恢复,并与其他协方差估计器进行比较。
- Visualizing the stock market structure: 真实股票市场数据示例,查找哪些信号最相关。
参考文献:
- Friedman et al, “Sparse inverse covariance estimation with the graphical lasso”, Biostatistics 9, pp 432, 2008
书籍推荐
