2.8. 收敛协方差

2.8.1. 基本收敛

尽管是协方差矩阵的无偏估计， 最大似然估计不是协方差矩阵的特征值的一个很好的估计， 所以从反演得到的精度矩阵是不准确的。 有时，甚至出现数学原因，经验协方差矩阵不能反转。 为了避免这样的反演问题，引入了经验协方差矩阵的一种变换方式：shrinkage 。

在 scikit-learn 中，该变换（具有用户定义的收缩系数） 可以直接应用于使用 shrunk_covariance 方法预先计算协方差。 此外，协方差的收缩估计可以用 ShrunkCovariance 对象 及其 ShrunkCovariance.fit 方法拟合到数据中。 再次，根据数据是否居中，结果会不同，所以可能要准确使用参数 assume_centered 。

在数学上，这种收缩在于减少经验协方差矩阵的最小和最大特征值之间的比率。 可以通过简单地根据给定的偏移量移动每个特征值来完成， 这相当于找到协方差矩阵的l2惩罚的最大似然估计器（l2-penalized Maximum Likelihood Estimator）。在实践中，收缩归结为简单的凸变换： .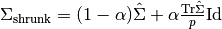

选择收缩量， 相当于设置偏差/方差权衡，下面将讨论。

示例:

• See Shrinkage covariance estimation: LedoitWolf vs OAS and max-likelihood for an example on how to fit a ShrunkCovariance object to data.

2.8.2. Ledoit-Wolf 收敛

在他们的 2004 年的论文 1(#id6) 中， O.Ledoit 和 M.Wolf 提出了一个公式， 用来计算优化的收敛系数 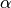， 它使得估计协方差和实际协方差矩阵之间的均方差进行最小化。

在 <cite>sklearn.covariance</cite> 包中，可以使用 ledoit_wolf 函数来计算样本的 基于 Ledoit-Wolf estimator 的协方差， 或者可以针对同样的样本 通过拟合 LedoitWolf 对象来获得。

例子:

• See Shrinkage covariance estimation: LedoitWolf vs OAS and max-likelihood 关于如何将 LedoitWolf 对象与数据拟合， 并将 Ledoit-Wolf 估计器的性能进行可视化的示例。

参考文献:

| 1(#id5) | O. Ledoit and M. Wolf, “A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices”, Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411. |

2.8.3. Oracle 近似收缩

在数据为高斯分布的假设下，Chen et al. 等 2(#id8) 推导出了一个公式，旨在 产生比 Ledoit 和 Wolf 公式具有更小均方差的收敛系数。 所得到的估计器被称为协方差的 Oracle 收缩近似估计器。

在 <cite>sklearn.covariance</cite> 包中， OAS 估计的协方差可以使用函数 oas 对样本进行计算，或者可以通过将 OAS 对象拟合到相同的样本来获得。

设定收缩时的偏差方差权衡：比较 Ledoit-Wolf 和 OAS 估计量的选择

参考文献:

| 2(#id7) | Chen et al., “Shrinkage Algorithms for MMSE Covariance Estimation”, IEEE Trans. on Sign. Proc., Volume 58, Issue 10, October 2010. |

示例:

• See Shrinkage covariance estimation: LedoitWolf vs OAS and max-likelihood for an example on how to fit an OAS object to data.
• See Ledoit-Wolf vs OAS estimation to visualize the Mean Squared Error difference between a LedoitWolf and an OAS estimator of the covariance.