title: 14. 经验风险最小化 date: 2019-01-05 13:53:00 categories: ERM tags: [ERM, 经验风险] mathjax: true

就线性分类模型而言，可以将其表示为： $$ h_\theta(x)=g(\thetaTx), \
g(z) = 1\lbrace z \geq 0 \rbrace $$ 其中，训练集表示为： $$ S=\lbrace (x{(i)}, y{(i)}) \rbrace _ {i = 1} m, (x{(i)}, y{(i)}) \sim {\cal D} $$ 这里假设了训练数据都是独立同分布的。

那么，我们认为，这个线性分类器的训练误差就可以表示为它分类错误的样本比例： $$ {\hat{\varepsilon}}(h_\theta) = {\hat{\varepsilon}}s(h\theta) = \frac{1}{m}\sum_{i=1}m1\lbrace h_\theta (x{(i)}) \neq y^{(i)} \rbrace $$ 在这里，我们把训练误差也称为风险（risk），由此我们导出了经验风险最小化。

经验风险最小化

Empirical Risk Minimization，ERM

经验风险最小化，最终导出一组参数，能够使得训练误差最小： $$ {\hat{\theta}} = \arg \min {\hat{\varepsilon}}s(h\theta) $$

我们再定义一个假设类${\cal{H}} = \lbrace h_\theta, \theta \in {\Bbb R}^{n+1} \rbrace$，它是所有假设的集合。在线性分类中，也就是所有线性分类器的集合。

那么，我们可以重新定义一次ERM： $$ {\hat h} = \mathop{\arg \min}_{h \in {\cal H}} {\hat \varepsilon}(h) $$ 对上述公式的直观理解就是：从假设类中选取一个假设，使得训练误差最小。我们这里用了$\hat{h}$表示估计，因为毕竟不可能得到最好的假设，只能得到对这个最好的假设的估计。

但这仍然不是目标，我们的目标是使得泛化误差 Generalization Error最小化，也即新的数据集上分类错误的概率： $$ \varepsilon(h)=P_{(x,y) \sim {\cal D}}(h(x) \neq y) $$ 接下去，为了证明：

• （1）${\hat \varepsilon} \approx \varepsilon$，训练误差近似于泛化误差（理解为，泛化误差和训练误差之间的差异存在上界）

• （2）ERM输出的泛化误差$\varepsilon({\hat h})$存在上界；

我们引出两个引理：

• 联合界引理（Union Bound）

  $A_1, A_2, \ldots , A_k$是k个事件，他们之间并不一定是独立分布的，有： $$ P(A_1 \cup \ldots \cup A_k) \leq P(A_1) + \dots + P(A_k) $$

• Hoeffding不等式（Hoeffding Inequality）

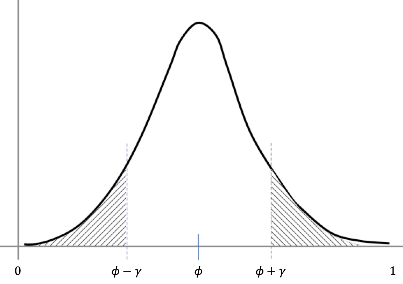
  $z_1, \ldots z_m$是m个iid（independent and identically distribution，独立同分布），他们都服从伯努利分布，$P(z_i=1) = \phi$，那么对$\phi$的估计： $$ {\hat \phi} = \frac{1}{m}\sum_{i=1}m z_i $$ 于是，给定$\gamma > 0$，有： $$ P(|{\hat{\phi}} - \phi| > \gamma) \leq 2 exp(-2\gamma2m) $$

  Hoeffding不等式的直观解释就是，下图中的阴影面积，会有上界。

  

一致收敛

Uniform Conversions

对于某个$h_j \in \cal{H}$，我们定义$z_i = 1 \lbrace h_j(x{(i)}) \neq y{(i)}\rbrace \in \lbrace{}$为第i个样本被分类错误的指示函数的值，对于logistic而言，它服从伯努利分布。

那么：

1. 泛化误差：$P(z_i=1) = \varepsilon(h_j)$
2. 训练误差：${\hat{\varepsilon}}(h_j) = \frac{1}{m}\sum_{i=1}^m z_i$

根据Hoeffding不等式，我们能够得到： $$ P(|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma) \leq 2e{-2\gamma2m} $$ 接着，我们定义训练误差和泛化误差之间的差大于$\gamma$（$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma$）为事件$A_j$，根据以上结论，我们可知： $$ P(A_j) \leq 2e{-2\gamma2m} $$ 那么根据联合界引理： $$ \begin{array}{l} & P(\exists h_j \in H, |{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma) \
= & P(A_1 \cup A_2 \cup \ldots \cup A_k) \
\leq & \sum_{i=1}k P(A_i) \
\leq & \sum_{i=1}k 2e{-2\gamma2m} \
= & 2ke{-2\gamma2m} \end{array} $$ 可以表述为：存在$h_j$使$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma$的概率$\leq 2ke{-2\gamma2m}$。

等价于：不存在$h_j$使$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| > \gamma$的概率$\geq 1 - 2ke{-2\gamma2m}$。

等价于：$\cal H$中任意的$h_j$使得$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \gamma$的概率$\geq 1 - 2ke{-2\gamma2m}$。

我们将上面这个结论称之为一致收敛 Uniform Conversions，也就是说事实上，所有的假设，训练误差和泛化误差之间都存在上界。

样本复杂度，误差界以及偏差方差权衡

上面的结论，我们可以引出以下的一些推论：

样本复杂度 Sample Complexity

给定$\gamma, \delta$，需要多大的训练集合（$m$）？其中$\delta$指的是泛化误差和训练误差之差大于$\gamma$的概率。

我们知道，$\delta \leq 2ke{-2\gamma2m}$，可求解： $$ m \geq \frac{1}{2 \gamma ^ 2} log(\frac{2k}{\delta}) $$ 这个，也被称为样本复杂度（类似于时间复杂度），指的是，只要满足上面这个条件，任意$h \in \cal H$，都能得到$|{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \gamma$

误差界 Error Bound

给定$\delta, m$时，我们会得到多大的误差上界$\gamma$。

经过求解可以得到： $$ P(\forall h \in {\cal H}, |{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \sqrt{\frac{1}{2m}log(\frac{2k}{\delta})}) \geq 1 - \delta $$ 也就是误差上界是：$\gamma = \sqrt{\frac{1}{2m}log(\frac{2k}{\delta})}$。

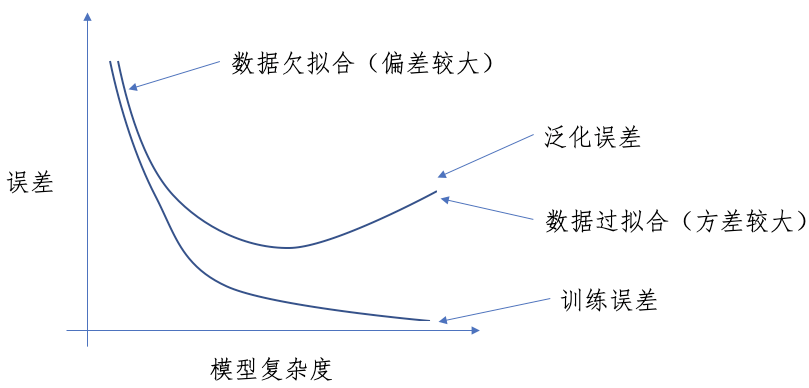
偏差方差权衡 Bias Variance Tradeoff

我们定义： $$ \begin{align} {\hat h} &= \mathop{\arg \min}{h \in \cal H} {\hat \varepsilon}(h) \text{, 使得训练误差最小的h} &\tag{1} \
h^\ast &= \mathop{\arg \min}{h \in \cal H} \varepsilon(h) \text{, 使得泛化误差最小的h} \tag{2} \end{align} $$ 假如： $$ \forall h \in {\cal H}, |{\hat{\varepsilon}}(h_j) - \varepsilon(h_j)| \leq \gamma \tag{3} $$

那么： $$ \begin{align} \varepsilon(\hat h) &\leq {\hat \varepsilon}({\hat h}) + \gamma, &\text{derived from (3)}\
&\leq {\hat \varepsilon}(h\ast) + \gamma, &\text{derived from (1)}\
&\leq {\varepsilon(h\ast)} + \gamma + \gamma, &\text{ derived from (3)} \end{align} $$ 于是，我们得到如下定理：

给定大小为$k$的假设集合$\cal H$，给定$m, \delta$，那么： $$ \varepsilon(\hat h) \leq \underbrace{(\min_{h \in {\cal H}}\varepsilon(h))}{\varepsilon(h^\ast)} + 2 \underbrace{\sqrt{\frac{1}{2m}log(\frac{2k}{\delta})}}{\gamma} $$ 的概率不低于$1-\delta$。

可以想象，为了得到最佳的假设$h\ast$，我们尽可能增大$\cal H$（能够减小$\varepsilon(h\ast)$），但随之而来的就是$\gamma$的增大，所以需要在这两者之间进行权衡，我们指的就是偏差方差权衡 Bias Variance Tradeoff。

由此，我们得到一个推论：

给定$\delta, \gamma$，为了能够保证$\varepsilon(\hat h) \leq (\min_{h \in {\cal H}}\varepsilon(h)) + 2\gamma$的概率不小于$1-\delta$（ERM得到的假设的一般误差，与最佳假设的一般误差之间，差值不大于$2\gamma$）

我们需要保证： $$ m \geq \frac{1}{2\gamma^2}log(\frac{2k}{\delta}) $$